k-nearest neighbors: Python code

Since data forms space and we are already familiar with distance and similarity measures, we can find points near a given point. Finding points near a point is called computing nearest neighbors. Given a data point, finding k closest points is called the computation of k-nearest neighbors. Finding k-nearest neighbors is also known as computing the knn. This article contains Python code from scratch to compute knn. Additionally, it provides an example of computing knn using the machine learning package scikit-learn in Python.

Problem statement for knn

Formally, the knn problem can be written as:

Given a vector $x$ and a data matrix $D$ , order all $n$ vectors of $D$ such that $D=\{x_1, x_2, x_3, \ldots, x_n\}$ and $\text{distance}(x, x_i)\leq\text{distance}(x, x_{i+1})$ . Return the first $k$ vectors $S=\{x_1, x_2, x_3, \ldots, x_k\}$ where $k\leq n$ .

For numerical objects, the length of $x$ must be equal to the number of features/dimensions in $D$ to be able to use a distance or similarity measure.

To make a program efficient, knn returns the indices (row serial number) of the top k-nearest neighbors, instead of returning k complete vectors from the data.

The distance function can be any proximity function that we are already familiar with from the previous lessons. You might need a distance measure for certain applications; for other applications, a similarity measure might be alright.

Example of knn

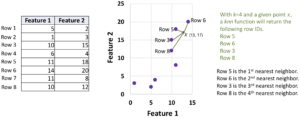
The table on the left side of the following figure has eight rows (objects) and two columns (features.) A point $x$ =(13, 17) is provided. We are attempting to find 4 nearest neighbors of $x$ in the data table. After computing distances between $x$ and each of the points, we found that Row 5 is the nearest point to $x$ . The second nearest point is Row 6 of the table. The third nearest point is Row 3. Row 8 contains the fourth nearest neighbor of $x$ . A 2D depiction of the points in space and the nearest neighbors are shown in the figure.

Computing k-nearest neighbors

The process to compute the nearest neighbors of a given point 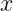$x$

To compute the k nearest neighbors of the given point $x$ =(13, 17) in the table above, we first computed the Euclidean distance of $x$ with each row of the data. The data point (or row) that has the smallest distance is the first nearest neighbor; the data point with the second smallest distance is the second nearest neighbor. When k=4, we select the rows for the first, second, third, and fourth in ascending order of the computed distance with $x$ .

The calculations are shown below.

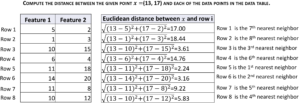
Computing k-nearest neighbors (knn)

For the example above, knn will return an array with content [5, 6, 3, 8], which indicates that Row 5 is the first nearest neighbor, Row 6 is the second nearest neighbor, Row 3 is the third nearest neighbor, and Row 8 is the fourth nearest neighbor.

Remarks

We used examples of two-dimensional data above because it is easy to visualize two-dimensional space. In reality, the data can have any number of dimensions. To use Euclidian distance to compute k-nearest neighbors, the given vector $x$ must have the same number of dimensions.

In the examples with the Python codes below, we use higher-dimensional data.

To find knn from string data, given a string one can compute the edit distance between the given string and each string object in the data.

Python coding to compute k-nearest neighbors

Given a vector, we will find the row numbers (IDs) of k closest data points. We will compute k-nearest neighbors–knn using Python from scratch.

We will create the dataset in the code and then find the nearest neighbors of a given vector. In the example, our given vector is Row 0.

knn from scratch using Python

Here is the code. The function name is nearest. It uses two other functions. One is euclid to compute the Euclidean distance between two data points or vectors. The other one is sortkey, which is the comparator for sorting indices based on distance.

#knn python code
import numpy as np

def euclid (vec1, vec2) :
    euclidean_dist = np.sqrt(np.sum((vec1-vec2)**2))
    return euclidean_dist

def sortkey (item):    
    return item[1]

def knearest (vec, data, k):
    result=[]
    for row in range(0, len(data)):
        distance=euclid(vec, data[row])
        result.append([row, distance])
    sortedResult= sorted(result, key=sortkey)
    indices=[]
    if k<len(data):
        for r in range(0, k):
            indices.append(sortedResult[r][0])
    else:            
        indices = [i[0] for i in sortedResult]
    return indices
    

# 7 Data points with each has 5 features
data = np.array([[10,3,3,5,10],
                  [5,4,5,3,6],
                  [10,4,6,4,9],
                  [8,6,2,6,3],
                  [10,3,3,5,8],                 
                  [9,2,1,2,11],
                  [9,3,1,2,11]])

referenceVec = data[0]; # We will find knn of Row 0

# Find 4 nearest neighbors of the reference vector
k=4
knn = knearest(referenceVec, data, k)
print("Row IDs of ", k, ' nearest neighbors:')
print(knn)

Once the Python script is executed, the output will be the following.

Row IDs of 4 nearest neighbors:
[0, 4, 2, 6]

Since we are finding the nearest neighbor of Row 0, the first nearest neighbor is Row 0 itself. Row 4, Row 2, and Row 6 are the second, the third, and the fourth nearest neighbors respectively.

knn using Python scikit-learn

scikit-learn on Python already has a function for computing k-nearest neighbors more efficiently using special data structures such as the ball tree. Here is an example of how we may use the NearestNeighbors class to find the nearest neighbors.

import numpy as np
from sklearn.neighbors import NearestNeighbors

# 7 Data points with each has 5 features
data = np.array([[10,3,3,5,10],
                  [5,4,5,3,6],
                  [10,4,6,4,9],
                  [8,6,2,6,3],
                  [10,3,3,5,8],                 
                  [9,2,1,2,11],
                  [9,3,1,2,11]])

# Find 4 nearest neighbors of the reference vector
k=4

# Reference vector
ReferenceVec=data[0]

## Using sklearn to find knn
nbrs = NearestNeighbors(n_neighbors=k, algorithm='ball_tree').fit(data)
distances, indices = nbrs.kneighbors([ReferenceVec])

# "distances" contains the nearest distance values for all k points
# "indices" contains the indices of the k nearest points

print("Row IDs of ", k, ' nearest neighbors:')
print(indices)

print("Distances of these ", k, ' nearest neighbors:')
print(distances)

The code shows how we can find the nearest neighbors of Row 0 (ReferenceVec). The indices variable provides the indices of the nearest neighbors of Row 0. The distances variable provides the distance between Row 0 and each of the rows in indices. The output of the program is provided below.

Row IDs of 4 nearest neighbors:
[[0 4 2 6]]
Distances of these 4 nearest neighbors:
[[0. 2. 3.46410162 3.87298335]]

9 Comments

Nonhlanhla

May 18, 2024

I had a problem computing the nearest euclidean distance for knn

Rex

August 9, 2023

The mathematical presentation is understandable but the coding aspect is hectic. Seems like cramming a pile of codes

sohail

June 29, 2023

its understandable for those having knowledge of vector space ,sets, matrices by now. Further lession will reveal what other knowledge of mathematics will required for data science.

Ekanem Mfon Kindness

December 5, 2020

wow! this lecture is awesome

Shahriar

December 6, 2020

I am glad to know that you liked the lecture. Thank you for visiting and commenting. Have a wonderful time.

Amin

July 21, 2020

No video presentation I don’t have maths background the only maths I did was a basic math the video presentation help some of us. Thanks

Shahriar

July 23, 2020

Thank you for your feedback. I understand that the videos are more detailed and demonstrate the techniques well. We will make more videos and new data science lessons in the coming months. Please stay tuned.

David W. Deemie

May 6, 2020

Thanks for the wonderful presentation!

Shahriar

May 6, 2020

Glad to know that you liked it. Have a wonderful day.

k-nearest neighbors: Python code

Problem statement for knn

Example of knn

The process to compute the nearest neighbors of a given point

Remarks

Python coding to compute k-nearest neighbors

knn from scratch using Python

knn using Python scikit-learn

9 Comments

Leave A Reply Cancel reply

Login with your site account

Register a new account

Modal title

The process to compute the nearest neighbors of a given point $x$