Evaluation of clustering algorithms: Measure the quality of a clustering outcome

Clustering evaluation refers to the task of figuring out how well the generated clusters are. Rand Index, Purity, Sum of Square Distance (SSD), and Average Silhouette Coefficient are widely used clustering evaluation metrics. These clustering assessment techniques fall under two categories: supervised evaluation, which uses an external criterion, and unsupervised evaluation, which uses an internal criterion. This page describes both types of clustering evaluation strategies.

Supervised evaluation of clustering using an external labeling/criterion

In supervised clustering evaluation, we already know what the cluster assignments should be for all the points. For validation purposes, we compare our clustering outcome with the known assignments. Therefore, supervised evaluation is driven by external labeling not used in the clustering algorithm. Most of the time, humans provide this external labeling with a benchmark dataset or a gold standard dataset.

A benchmark dataset or a gold standard dataset is a dataset for which the expected outcome is provided. We use the benchmark dataset to validate the correctness of an algorithm by comparing the result of an algorithm with the expected outcome. The term gold standard has many different names. Sometimes, you might hear the terms: true labels, reference data, ground truth, truth set, actual labels, real annotations, verified data, correct classifications, and baseline data. All of these terms are generally referring to the benchmark dataset.

As we know, cluster assignments computed by an algorithm like k-means simply form an array or a vector. The length of the assignment vector is equal to the number of objects/data points/rows in the data table. Each element of the assignment vector tells us what the cluster ID of the corresponding row in the dataset is. Additionally, the known assignments also form a vector. The known assignments or gold set assignments are also called labels. A supervised clustering evaluation technique attempts to discover the amount of match between the assignments derived from a clustering algorithm and the known assignments.

Complications associated with an external criterion

For the dataset provided in Figure 1, cluster assignments resulting from k-means exactly match the known assignments or expected assignments, or ground-truth assignments. Any supervised evaluation should identify this match as a perfect match. The clusters are drawn by two ellipses on the right side of Figure 1.

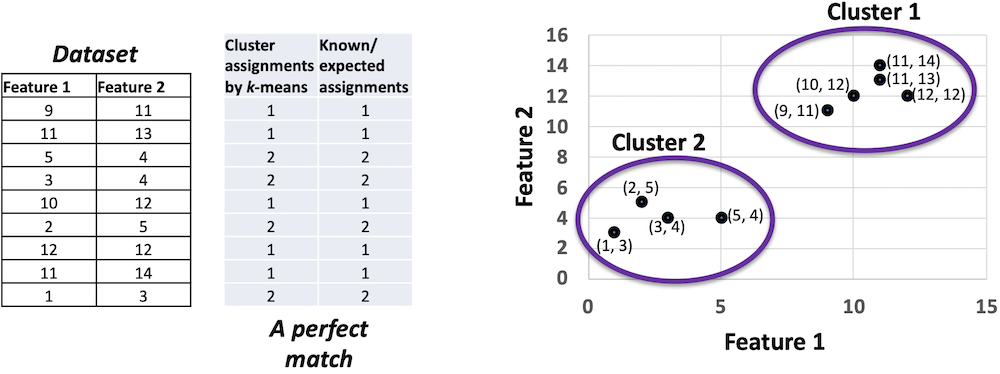
Evaluation of clustering — **Figure1:** An example of a perfect match between k-means clustering outcome and known cluster assignments.

While Figure 1 demonstrates a 100% assignment-wise match between the k-means outcome and the gold set, there can be another scenario for the same dataset where each of the k-means assignments is different from the known assignments but yet the cluster-wise matching is 100% perfect. How is that possible?

Consider that k-means has flipped the Cluster IDs. That is Cluster 1 is now called Cluster 2 and Cluster 2 is now called Cluster 1 in the k-means outcome. The k-means outcome is still correct but there is no direct match with the known assignments now. Should we consider that k-means is producing incorrect results? The answer is — No. When the k-means algorithm gives us a result it tells us which rows in the data belong to which cluster. Whatever it calls Cluster 1 now, it may call it by another ID next time we execute the algorithm with the same data. All that matters is if the same set of points are in one cluster as the known assignments. Figure 2 explains the scenario further.

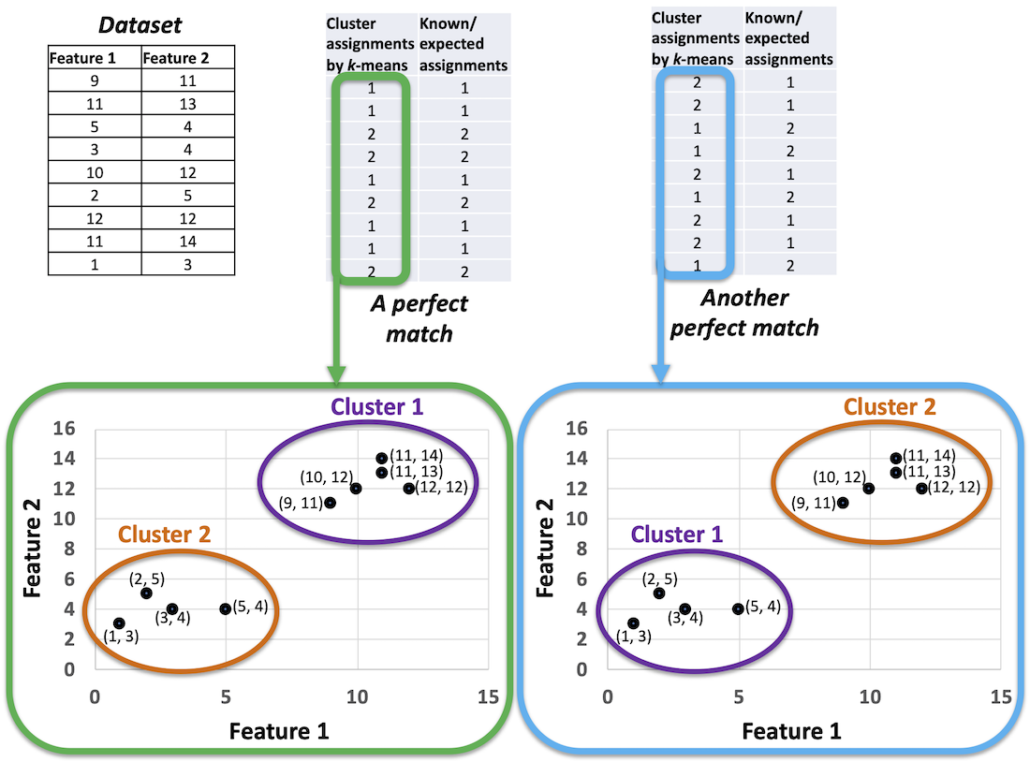
Two clustering results with perfect match. — **Figure 2:** Two different clustering results that have a perfect match with the known assignments. In these two clustering outcomes, the assignments are flipped. That is, Cluster 1 of the results on the left side is called 2 in the results on the right side. Similarly, Cluster 2 of the results on the left side is called Cluster 1 in the results on the right side. Both are correct results because they are for the same two clusters on the left and right sides. It does not matter what we call these two clusters Cluster 1, Cluster 2, or Cluster 2, Cluster 1, or Apple, Oranges, or Cats, Dogs.

That is, all the points of each cluster given by a clustering algorithm should be in one cluster of the known assignments, to consider that there is a perfect match. Therefore, when we design our evaluation metric, we should keep into consideration that cluster-ID is just a number and should not be compared with known assignments directly.

We will discuss two supervised clustering evaluation metrics — Rand index and Purity.

Rand index for evaluation of clustering

Rand index measures how similar two sets of clustering results are. We use the Rand index to evaluate the outcome of a clustering algorithm by comparing the outcome with a known or expected outcome.

As discussed, direct matching between cluster IDs of an algorithmic outcome and the expected clustering is not an option in the evaluation of clusters. Evaluation of clustering should be performed using assignments of each pair of points. For example, with a correct clustering outcome, if a pair of points are in the same cluster in the gold set, the pair should be in the same cluster created by the algorithm too. If a pair of points are in two different clusters in the gold set, then the pair should be in two different clusters in the clusters created by the algorithm too. Therefore, the more agreements are there between pairs of points in the algorithmic outcome and the gold set, the higher the correctness is.

Positive pairs: If a pair of points are in the same cluster created by a clustering algorithm, the pair is called a positive pair.

Negative pairs: If a pair of points are in two separate clusters created by a clustering algorithm, then the pair is called a negative pair.

In a correct clustering algorithm, we expect that the positive pairs are also positive in the gold set. Similarly, a negative pair of points are expected to be in two different clusters in the gold set.

True-positive: If a pair of points are in the same cluster in the clustering created by the algorithm and in the gold set, then the pair is called a true-positive pair.

True-negative: If a pair of points are in two different clusters in the clustering created by the algorithm and also in the gold set, then the pair is called a true-negative pair.

False-positive: If a pair of points are in the same cluster in the clustering created by the algorithm but in separate clusters in the gold set, then the pair is called a false-positive pair.

False-negative: If a pair of points are in two separate clusters in the clustering created by the algorithm but in the same cluster in the gold set, then the pair is called a false-negative pair.

Rand index is the ratio between all true events and all pairs. That is,

$\text{Rand index}=\frac{\text{\#True poitives+\#True negatives}}{\text{\#True poitives+\#True negatives+\#False positives+\#False negatives}}$

A Rand index of 1.0 indicates a perfect match in clustering. Lesser values indicate some errors. With both the clustering results of Figure 2, the Rand index will be 1.0.

Python code to compute Rand index

The video that explains the implementation of the Rand Index using Python is as follows. Throughout the video, I use a simple toy dataset to demonstrate how to apply the KMeans clustering algorithm, and subsequently, how to use our implemented Rand Index to evaluate the clustering outcome against the ground truth.

A Python function to compute the Rand index between a clustering outcome and the expected outcome is provided below.

import numpy as np
from sklearn.cluster import KMeans

def RandIndex(result, gt):
    TP=0
    TN=0
    FP=0
    FN=0
    
    for i in range(0, len(result)-1):
        for j in range(i+1, len(result)):
            if ( result[i]==result[j]):
                # Positive pair
                if (gt[i]==gt[j]):
                    #True
                    TP=TP+1
                else: #False
                    FP=FP+1
            else: # Negative pair
                if (gt[i]==gt[j]): # False
                    FN=FN+1
                else: # True 
                    TN=TN+1
    
    RI= (TP+TN)/(TP+TN+FP+FN)
    return RI

if __name__ == "__main__":
    
    rawData=[[5, 1, 2, 3],
             [4, 0, 3, 4],
             [20, 20, 15, 7],
             [11, 12, 8, 8],
             [20, 20, 15, 7]]
                 
    data=np.array(rawData)
    
    k=3 # Number of clusters
    
    km = KMeans(n_clusters=k).fit(data)
    clusteringOutcome = km.labels_
    groundTruth = [2, 2, 1, 1, 3]
    
    print("Clustering result:\n", clusteringOutcome)
    print("Ground truth:\n", groundTruth)
    
    
    rand=RandIndex(clusteringOutcome, groundTruth)
    print("Rand Index: ", rand)

Purity for evaluation of clustering

Purity is another evaluation of clustering that utilizes an external criterion. To compute purity, each cluster of the algorithmic outcome is assumed to be the cluster that holds the most points from the clusters of the gold set. For example, Cluster 1 of the algorithmic outcome will be considered Cluster 2 of the gold set if most of the points of algorithmic Cluster 1 are marked as Cluster 2 of the gold set. Purity is then computed as a ratio of the summation of how many maximum points of each algorithmic cluster match with a considered gold set cluster and the total number of points in data.

If there are k algorithmic clusters, $c_1, c_2, \ldots, c_k$ and t gold set clusters $g_1, g_2, \ldots, g_t$ , then purity is computed using the following formula.

$\text{Purity}(\text{algorithmic clusters}, \text{gold-set clusters})$

$= \frac{\sum_{i=1}^{k}\max_{j=1}^{t}\left ( c_i \cap g_j \right ) }{N}$

The higher the purity the better the clustering outcome is. The maximum purity value is 1.0.

Example: Assume that we have a dataset with 14 data points for which we already know the expected cluster assignments. We run a clustering algorithm, such as k-means, with k=3, and we receive the assignment vector for the 14 points. Both the outcome of the clustering algorithm and the expected cluster assignments are provided in the following table.

Clustering output	2	1	1	3	2	2	2	3	2	1	1	3	3	2
Gold set/ expected	1	2	2	2	1	1	1	3	2	2	1	3	1	2

We will compute the purity of the output as an evaluation of clustering.

Cluster 1 of the clustering output has 1 match with Cluster 1 of the gold set. Cluster 1 of the clustering output has 3 matches with Cluster 2 of the gold set. Finally, Cluster 1 of the clustering output has zero matches with Cluster 3 of the gold set. The maximum count of match is 3 for Cluster 1 of the clustering output.

Cluster 2 of the clustering output has 4 matches with Cluster 1 of the gold set. Cluster 2 of the clustering output has 2 matches with Cluster 2 of the gold set. Finally, Cluster 2 of the clustering output has zero matches with Cluster 3 of the gold set. The maximum match is 4 for Cluster 2 of the clustering output.

Cluster 3 of the clustering output has 1 match with Cluster 1 of the gold set. Cluster 3 of the clustering output has 1 match with Cluster 2 of the gold set. Finally, Cluster 3 of the clustering output has 2 matches with Cluster 3 of the gold set. The maximum match is 2 for Cluster 2 of the clustering output.

Counting the maximum matches, for each cluster of the clustering output, we have 3+4+2=9 in the numerator of the formula for purity. The denominator will be 14 because we have 14 data points (hence, the length of each assignment vector is 14.) Therefore, the purity of the clustering outcome of this example is 9/14=0.642857142857143.

Python code to compute Purity

A Python function to compute the Purity of a clustering outcome (assignment) given the expected result (known) is provided below.

def Purity(assignment, known):
    aLabels = set(assignment)
    aLabels = list(aLabels)
    kLabels = set(known)
    kLabels=list(kLabels)

    maxOverlaps = []

    for cID in aLabels:
        indicesOfCID = [ii for ii in \
            range(0, len(assignment)) if \
             assignment[ii]==cID]
        overlap=[]

        for ckID in kLabels:
            indicesOfCkID = [ii for ii in \
            range(0, len(known)) if \
             known[ii]==ckID] 
            overlap.append(\
            len(set(indicesOfCID).intersection(indicesOfCkID))\
            )
        maxOverlaps.append(max(overlap))

    purity = sum(maxOverlaps)/len(assignment)
    return purity

Unsupervised evaluation of clustering using an internal criterion

In unsupervised clustering, we do not know what the clustering assignments should be. That is, we do not have a gold set to compare with. Therefore, we cannot directly say how accurate the clustering outcomes are. In unsupervised clustering evaluation, we rely on how well the structure of each cluster is. A cluster with points that are very close to each other is considered a good cluster (due to the intra-cluster distance objective.) Also, in good clustering results, a pair of points from two different clusters should have a large distance (due to inter-cluster distance objective). Unsupervised evaluation metrics generally leverage intra-cluster and/or inter-cluster distance objectives of a clustering outcome.

The sum of squared distance for evaluation of clustering

The sum of the squared distance between each point and the centroid of the cluster it is assigned to is a local measure to compute clustering quality. Let $x_i$ be the ith point, and $\mu_{x_i}$ be the centroid of the cluster $x_i$ is assigned to. Then the sum of squared distance (SSD) for N data points is computed using the following formula.

$\text{SSD}=\sum_{i=1}^{N} \left \| x_i-\mu_{x_i} \right \|^2$

The sum of squared distance can be used to compare the quality of the clustering outcomes of different executions of the same algorithm for the same data with the same number of clusters. For example, the k-means clustering algorithm might give different clustering outcomes in different runs using the same data with the same k. While this is uncommon when the dataset has clear and well-separable clusters, with complex and overlapping groups of points there might be multiple locally optimum clustering outcomes. It is a common practice to execute the k-means clustering algorithm many times and pick up a few clustering outcomes with the smallest SSD values.

Lower SSD values indicate better results. Lower SSD indicates that the points are not that far away from the centroids they are assigned to. Theoretically, the best SSD value is 0.0. SSD is can become zero only when all points in a cluster are exactly equal to the centroid. That means, SSD=0.0 when the distance between each point and its corresponding cluster-centroid is 0.0.

Average Silhouette Coefficient for the evaluation of clustering

The Silhouette Coefficient of a data point takes into account both the intra-cluster distance and the inter-cluster distance in evaluating a clustering outcome. It is an unsupervised clustering evaluation with an internal criterion. If $a$ represents the intra-cluster distance of a data point and $b$ represents the inter-cluster distance, then the Silhouette Coefficient of the point is considered $(b-a)/\max{(a, b)}$ .

Let the clusters be $C_1, C_2, \ldots , C_k \in C$ . The mean intra-cluster distance of the ith data point $x_i$ residing in cluster $C_{x_i}\in C$ is computed using the following formula.

$a(x_i)=\frac{1}{|C_{x_i}|-1}\sum_{x_j\in C_{x_i}, i\ne j}\left \| x_i-x_j \right \|$

The mean inter-cluster distance of the ith data point $x_i$ is computed by taking the minimum of the mean of the distances between $x_i$ and all the data points of the cluster that is not $C_{x_i}$ .

$b(x_i)=\min_{C_k\in C, C_k\ne C_{x_i}}\frac{1}{|C_k|}\sum_{x_j\in C_k}{\left \| x_i-x_j \right \|}$

The Silhouette Coefficient of data point $x_i$ is computed as:

$s(x_i)=\frac{b(x_i)-a(x_i)}{\max \{a(x_i), b(x_i) \}}$

The equation will give Silhouette Coefficient for each data point. A negative silhouette value would indicate that the intra-cluster distance is larger than the inter-cluster distance. That would indicate that the data point is not in a cluster but rather in a random space where there is no structure.

A positive Silhouette Coefficient value of a data point indicates that the point is in a cluster that is separable from other clusters. That means the intra-cluster distance is smaller than the inter-cluster distance. Note that the inter-cluster distance ( $b(x_i)$ ) is actually the mean distance with points of possibly the nearest cluster. Therefore, the positive Silhouette Coefficient indicates that the point $x_i$ is inside a cluster.

A Silhouette Coefficient value of 0.0 indicates that the point is probably on the border of a cluster that overlaps a little with another cluster.

Higher Silhouette Coefficient values for all data points are expected. To compute the overall quality of a clustering outcome, Silhouette Coefficients are averaged over all the points. That is the Average Silhouette Coefficient (ASC) for a dataset with N data points is computed using the following formula.

$ASC$ $= \frac{1}{N}\sum_{i=1}^{N} s(x_i)$

ASC may vary between -1.0 to 1.0.

Negative ASC indicates that the clustering outcome does not provide any sort of structure.

Positive ASC indicates that the clustering outcome has some sort of structure. The larger the ASC is the better the clusters are.

An ASC value of 0.0 indicates that all points are scattered in the space such that all points seem to be on the boundary of a cluster.

Other (unconventional) methods to evaluate clustering

Some unconventional methods to evaluate clustering results are as follows.

Visual inspection:

This involves visualizing the clustering results through techniques such as scatter plots and dendrograms to assess the quality of the clusters.

Domain knowledge:

This involves using domain-specific knowledge and intuition to evaluate the results. For example, in a medical imaging application, a radiologist may assess the quality of the clusters based on their medical expertise.

Ensemble methods:

This involves combining multiple clustering algorithms and using consensus-based approaches, such as majority voting, to obtain a final clustering result. The quality of the final result can be evaluated using the Silhouette score, Calinski-Harabasz index, and Davies-Bouldin index, or visual inspection or domain knowledge.

External validation:

Another clustering evaluation technique neither uses ground truth nor utilizes the data alone. That is called External validation. This involves comparing the clustering results with some external criteria. For example, let us consider we have a cluster of people based on health-related features. Do most people in a cluster fall under a specific geographical region, even though the clustering algorithm did not use geographic location? That would imply that a group with similar health conditions is associated with a particular area. This sort of External validation approach requires domain knowledge about the data and beyond. This external validation approach is at the core of many research efforts.

4 Comments

mya thidar kyaw

March 6, 2023

I would like to know methods for evaluation of Agglomerative Hierarchical Clustering. Please guideline to me.

M. Shahriar Hossain

March 6, 2023

Thank you for your question.

There is a metric called, the Cophenetic correlation coefficient, specific to evaluating hierarchical agglomeration clustering. The Cophenetic correlation coefficient measures the correlation between the pairwise distances of the original data points and the pairwise distances of the clusters formed by the hierarchical clustering algorithm. It is based on the cophenetic distance matrix, which is a matrix of the pairwise distances between the clusters at each level of the hierarchical clustering tree.

I did not cover the Cophenetic correlation coefficient in this course.

If your data has ground truth cluster labels, you can use the Rand index and purity for both hierarchical and k-means clustering. If you do not have ground-truth labels, then Average Silhouette Coefficient also seems like a reasonable choice to evaluate hierarchical agglomeration clustering.

abdul

June 28, 2021

That was a great explanation . Thank you .