PageRank Algorithm

This article on PageRank algorithm is accompanied by the following YouTube videos for clarity! In the videos, I minimize technical language to ensure the content is easily understood.

Part 1. Creating the Transition Matrix for the Internet: How Google Search Works:

Part 2: Iterating Over the PageRank Vector to Rank Web Pages: How Google Search Works:

Part 3: Pseudocode, Spider Trap, and How Google Search Engine Works:

Part 4: Random Surfer Model and Spider Trap: How Google Search Works with Spider Traps:

Part 5: Teleportation Details with Pseudocode: How Google Solves the Spider Trap Issue:

Part 6: Implementing PageRank Algorithm in Python | Handling Spider Traps and Teleportation:

The PageRank algorithm, introduced by Larry Page and Sergey Brin in 1996, has profoundly impacted how search engines function. Its core principle is assessing the importance of web pages based on the number and quality of incoming links. This algorithm has been a cornerstone of Google’s search engine since its inception and continues to influence search engine optimization (SEO) strategies.

In this article, we will dive deep into the PageRank algorithm, dissecting its matrix formulation and discussing the introduction of teleportation to account for the “random surfer” model. By the end of this article, you will have a solid understanding of the PageRank algorithm, how it operates, and how to implement it using Python.

Fundamental Assumption

The PageRank algorithm is a sophisticated method of evaluating the importance of web pages by examining their linking structure. It operates under the premise that significant pages are more likely to receive more inbound links from other pages. To understand how PageRank works, it is essential to delve into its key components, including the link structure of the web and the random surfer model.

Link Structure of the Web

The World Wide Web consists of numerous interconnected web pages linked by hyperlinks. These hyperlinks create a complex network where each page serves as a node, and the links between the nodes act as connections. The PageRank algorithm uses this link structure to analyze the relationships between pages and determine their relative importance.

Inbound Links: Also known as backlinks, inbound links are hyperlinks pointing to a web page from other pages. Pages with more inbound links are considered more important, as they are often cited or referred to by other pages.

Outbound Links: These are the links on a web page that point to other pages. The PageRank algorithm considers the number of outbound links on a page when distributing the importance (so-called PageRank juice) of that page to other connected pages.

Random Surfer Model

The random surfer model is a conceptual foundation of the PageRank algorithm. It simulates the behavior of an internet user who navigates the web by randomly clicking on links. The model assumes that users are more likely to visit important pages since they have more inbound links. As the user follows the links, the likelihood of landing on a particular page corresponds to its PageRank value.

Later in this article, we will see that the random surfer model also considers the possibility of a user jumping to a random page rather than following only links/hyperlinks. A damping factor captures this behavior, typically set at 0.85. The damping factor represents the probability of the random surfer continuing to follow links, while the remaining probability (1 – damping factor) accounts for the user jumping to a random page.

Basic/Vanilla PageRank Algorithm

The basic PageRank algorithm can be mathematically represented using matrix notation. Let’s begin by defining a few key terms first:

N: The total number of web pages
A: The adjacency matrix of the web graph, where A(i, j) = 1 if there is a link from page j to page i, and 0 otherwise. Notice that an outbound edge is encoded from a column index to a row index.
M: The transition matrix, where M(i, j) = A(i, j) / Out(j), and Out(j) is the number of outbound links from page j. Notice here that each column will sum up to one in M. Therefore, the transition matrix, M, is column-stochastic.
r: The PageRank vector of length N, where r(i) represents the PageRank of the ith web page.

Now, let us define the matrix formula for the basic PageRank algorithm:

r = Mr

Notice that M is an N*N matrix, and r is a column vector of length N. For clarity, the equation above can be written programmatically as:

r_new=r_prev=[Uniform rank vector with all equal values of 1/N]
While (true): # Infinite loop
    r_new = M*r_prev
    If (r_new and r_prev are almost equal)
        break
    r_prev=r_new

This matrix multiplication is iteratively solved. The vector, r, converges to a steady-state vector (when r_new is almost equal to r_prev), which represents the final page ranks. The resulting page ranks determine the order in which web pages appear in search results.

As an example, let us assume that we have the following network. Website A links to websites B, C, and D (outbound links from A to B, A to C, and A to D); B links to C (outbound link from B to C); C links to A (outbound link from C to A); D links to B and C (outbound links from D to B and D to C).

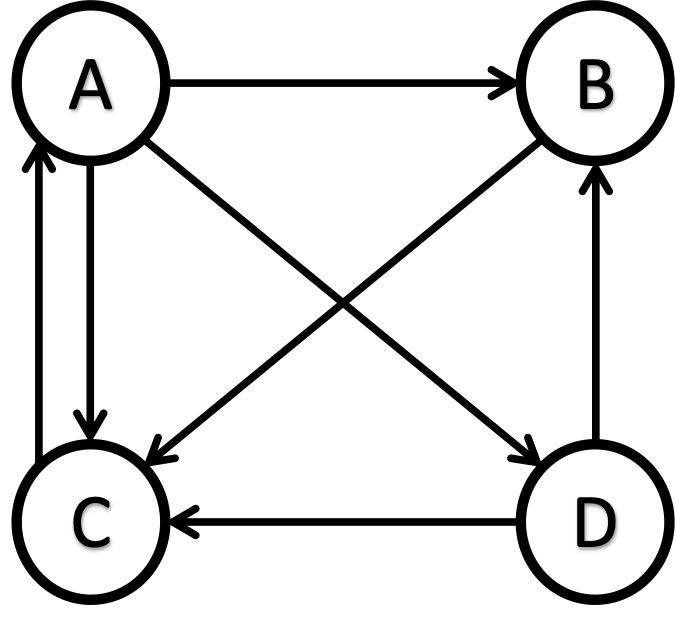
PageRank Algorithm — Figure: Let us call this network “Our Good Network.”

The corresponding adjacency matrix for Our Good Network is as follows.

–	A	B	C	D
A	0	0	1	0
B	1	0	0	1
C	1	1	0	1
D	1	0	0	0

The corresponding transition matrix, M, is provided below.

–	A	B	C	D
A	0	0	1	0
B	1/3	0	0	1/2
C	1/3	1	0	1/2
D	1/3	0	0	0

The initial rank vector is:

r_prev = [1/4, 1/4, 1/4, 1/4]

Iteration 1:

r_new = M * r_prev
r_new =
  [[0, 0, 1, 0 ] * [1/4, 1/4, 1/4, 1/4]
  [1/3, 0, 0, 1/2 ]
  [1/3, 1, 0, 1/2 ]
  [1/3, 0, 0, 0 ]]

r_new = [0.25, 0.20833333, 0.45833333, 0.08333333]
r_prev=r_new

Iteration 2:

r_new = M * r_prev
r_new = 
  [[0, 0, 1, 0 ] * [0.25, 0.20833333, 0.45833333, 0.08333333]
  [1/3, 0, 0, 1/2 ] 
  [1/3, 1, 0, 1/2 ] 
  [1/3, 0, 0, 0 ]]

r_new = [0.45833333, 0.125, 0.33333333, 0.08333333]
r_prev=r_new

Iteration 3:

r_new = M * r_prev 
r_new = 
  [[0, 0, 1, 0 ] * [0.45833333, 0.125, 0.33333333, 0.08333333]
  [1/3, 0, 0, 1/2 ] 
  [1/3, 1, 0, 1/2 ] 
  [1/3, 0, 0, 0 ]]
 
r_new = [0.33333333, 0.19444444, 0.31944444, 0.15277778]
r_prev=r_new

After 71 such iterations, the rank vectors r_prev and r_new will become almost equal. It will be the following one.

[0.35294118, 0.17647059, 0.35294118, 0.11764706]

It indicates that webpages A and C are equally important and have the highest importance (0.35294118). Website B is of the next importance (0.17647059). Website D has the least importance (0.11764706).

The equation r=M*r might suffer from a spider trap issue. A spider trap happens when a website is structured to allow web crawlers to follow a series of links, causing the crawler to revisit the same page(s) repeatedly without finding new content. With one page linking only to itself, all the PageRank values can end up on that page. For example, the following network has a spider trap at node D.

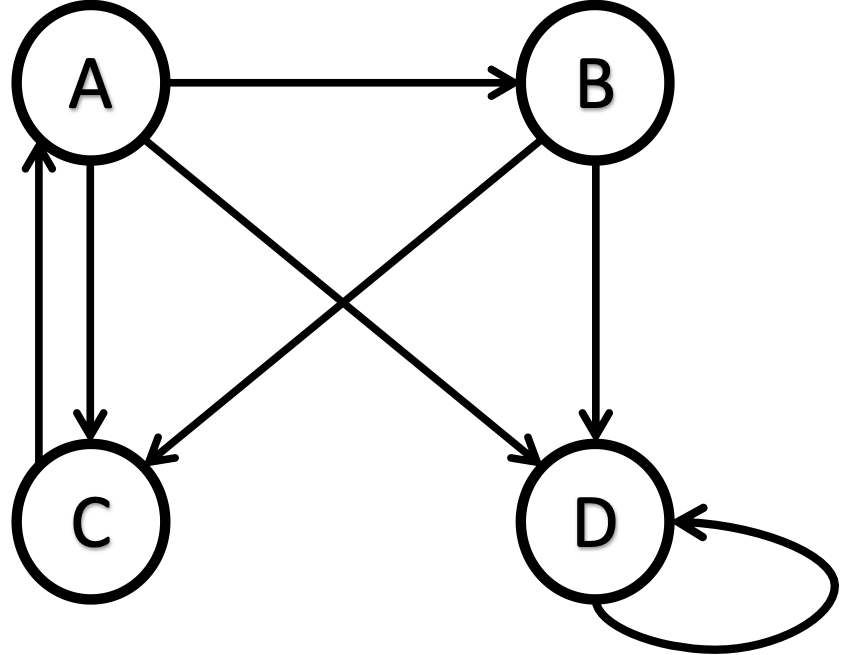
If you apply PageRank on this network, you will converge at [0, 0, 0, 1] rank vector using the basic PageRank algorithm we have discussed. That is, since D has a self-loop and no outgoing link, all the PageRank juice will end up in D, giving an illusion that D is the most important webpage and A, B, and C are entirely unimportant.

Additionally, there can be an issue of a dangling node. A dangling node is a web page with no outgoing links, meaning that PageRank flows into the page but cannot pass any PageRank to other pages. Dangling nodes can cause problems in calculating PageRank scores because they break the connectivity of the link graph. The dangling node’s column in the adjacency matrix A will have only zeros, giving a division by zero error when doing this computation: A(i, j) / Out(j), during the computation of M. For example, D is a dangling node in the following network.

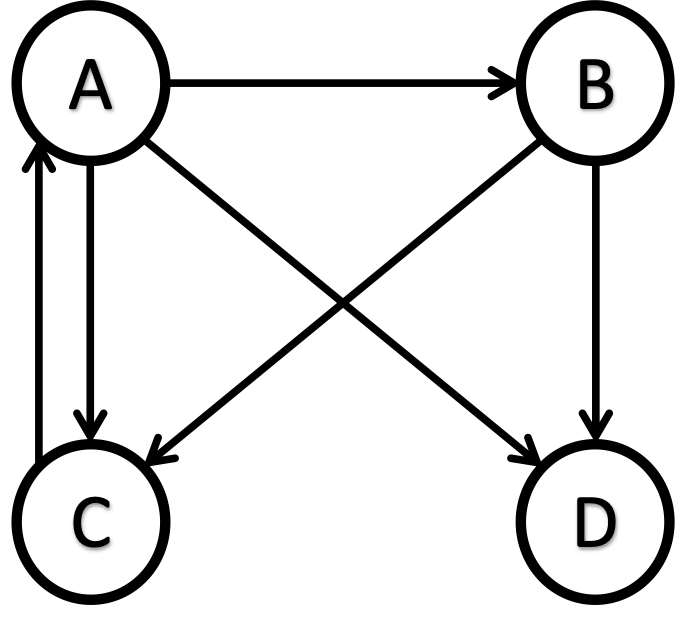
D is a dangling node.

The term “dead end” is often used interchangeably with the term “dangling node” in the context of web page links and graph theory.

While the dangling nodes can be detected easily and removed from consideration, spider traps are a little more challenging to handle, especially when a small group of web pages tries to keep the PageRanks to themselves artificially (and, of course, decisively).

To resolve the issue of Spider Trap, the basic PageRank algorithm introduces the concept of random teleportation.

PageRank Algorithm with Random Teleportation

To address the spider trap problem, we can introduce random teleportation, which allows the random surfer to jump to any page on the web with a certain probability instead of being trapped within closed loops. This is achieved by adding a damping factor ( $\beta$ ) and a teleportation matrix U.

Teleportation is introduced by adding a teleportation matrix, U, to the equation. The teleportation matrix represents the probability of a user jumping to any random page on the web. The simplest teleportation matrix U can be considered a column-stochastic version of an adjacency matrix with all 1’s in all cells. That is, each cell of the teleportation matrix contains the value 1/N, where N is the number of web pages.

U ensures that the random surfer has an equal probability of jumping to any page on the web. The damping factor ( $\beta$ ) is typically set to 0.85.

The modified PageRank equation with teleportation is:

$r = \beta Mr + (1 - \beta) Ur$

Given that U is uniform and r is a rank vector that sums up to 1.0, the resultant rank vector with the multiplication of Ur will always be a unique rank vector with the content $\left[\frac{1}{N}, \frac{1}{N}, \frac{1}{N}, \dots, \frac{1}{N}\right]^T = \frac{1}{N} \times [\overrightarrow{1}]^T$ of length N. The T in the vector ensures a column vector representation instead of a row.

That is, $Ur=\frac{1}{N} \times [\overrightarrow{1}]^T$

Therefore, the modified PageRank equation with teleportation becomes:

$r = \beta Mr + (1 - \beta) \frac{1}{N} \times [\overrightarrow{1}]^T$

Notice that $(1 - \beta) \frac{1}{N} \times [\overrightarrow{1}]^T$ is a one-time computation that will not change over the iterations and hence can be precomputed.

The pseudocode becomes:

r_new=r_prev=[Uniform rank vector with all equal values of 1/N]
v=(1-beta)*r_new
While (true): # Infinite loop
    r_new = beta*M*r_prev+v
    If (r_new and r_prev are almost equal)
        break
    r_prev=r_new

This new equation accounts for the probability of $(1 - \beta)$ that a user may jump to a random page.

Now consider Our Good Network again, for which the transition matrix M was:

–	A	B	C	D
A	0	0	1	0
B	1/3	0	0	1/2
C	1/3	1	0	1/2
D	1/3	0	0	0

with $\beta=0.85$

$(1 - \beta) \frac{1}{N} \times [\overrightarrow{1}]^T$ will be

$v=(1 - 0.85) [0.25, 0.25, 0.25, 0.25] =0.15 * [0.25, 0.25, 0.25, 0.25]=[0.0375, 0.0375, 0.0375, 0.0375]$

Running iterations over:

r_new = beta*M*r_prev+v

we will observe the following rank vectors:

After Iteration 1:

[0.25, 0.21458333, 0.42708333, 0.10833333]

After Iteration 2:

[0.40052083, 0.154375, 0.33677083, 0.10833333]

After Iteration 3:

[0.32375521, 0.19702257, 0.32824132, 0.1509809 ]

………………… ………….. …………………

After convergence with Our Good Network:

[0.33286614, 0.1878322, 0.34748958, 0.13181207]

If you apply the updated PageRank algorithm with random teleportation on “Our Spider Trap Network,” instead of [0, 0, 0, 1], you will converge at [0.12624893, 0.07327053, 0.10441051, 0.69607004] with beta=0.85. Even though D still has the highest rank, A, B, and C now have comparable PageRank values instead of zeros.

We have mentioned the word convergence several times in this article but haven’t yet discussed how it works in the PageRank algorithm. Here is how convergence works in the PageRank algorithm.

The Convergence of the PageRank Algorithm

The part

"If (r_new and r_prev are almost equal)"

in out pseudocode refers to the convergence of the algorithm.

To ensure that the iterative process of the PageRank algorithm converges to a stable set of PageRank values, we need to establish a convergence criterion. One commonly used criterion is the difference between the PageRank vectors of two consecutive iterations.

Given two consecutive PageRank vectors r(t) and r(t+1) at iterations t and t+1, or, as used in our pseudocode, r_new and r_prev, we can calculate the difference between these two vectors using a suitable norm, such as the L1 norm or the L2 norm.

L1 Norm (Manhattan Norm)

The L1 norm calculates the absolute difference between the corresponding elements of two vectors and sums them up. The formula for the L1 norm is:

L1_norm(r(t+1), r(t)) = $\sum_1^N(|r(t+1)[i] - r(t)[i]|)$

for i = 1, 2, …, N, where N is the number of web pages.

L2 Norm (Euclidean Norm)

The L2 norm calculates the squared difference between the corresponding elements of two vectors, sums them up, and takes the square root of the result. The formula for the L2 norm is:

L2_norm(r(t+1), r(t)) = $\sqrt{ \sum_1^N\left (|r(t+1)[i] - r(t)[i]|\right )^2}$

for i = 1, 2, …, N, where N is the number of web pages.

To determine convergence, we compare the calculated norm with a predefined threshold (e.g., ε = 0.001 or any small positive value). If the norm is less than the threshold, we consider the PageRank values to have converged:

L1_norm < ε, or

L2_norm < ε

Once the convergence criterion is met, we can stop the iterative process and use the PageRank vector from the last iteration as the final set of PageRank values, representing the relative importance of the web pages.

The pseudocode can be modified (let’s say, using L1_norm):

r_new=r_prev=[Uniform rank vector with all equal values of 1/N]
v=(1-beta)*r_new
While (true): # Infinite loop
    r_new = beta*M*r_prev+v
    diff=L1_norm(r_new, r_prev)
    If (diff<)
        break
    r_prev=r_new

Python code for PageRank Algorithm

Here is my simple Python code for PageRank algorithm. I used this code for the calculations I showed on this page. Change threshold, beta as needed. A is the adjacency matrix in which outgoing links must be encoded from columns to rows.


import numpy as np

threshold = 0.0000000000001
beta =0.85

'''
# Our Good Network
A=[[0,0,1,0],
   [1,0,0,1],
   [1,1,0,1],
   [1,0,0,0]]
'''

# Our Spider Trap Network
A=[[0,0,1,0],
   [1,0,0,0],
   [1,1,0,0],
   [1,1,0,1]]

arr=np.array(A, dtype=float)

s=[]

for i in range(0, len(A)):
    s.append(np.sum(arr[:,i]))



print("Summation of columns: ", s)   

M=arr

for j in range(0, len(A)):
    M[:,j]=M[:,j]/s[j]

print("Column stochastic probability matrix, M:")
print(M)

r=(1.0+np.zeros([len(M), 1]))/len(M)

print("Initial rank vector:")
print(r)

uniformR=(1.0-beta)*r

r_prev=r

for i in range(1, 1001):
    print("Iteration: ", i)
    r=beta*np.matmul(M, r_prev)+uniformR
    
    print("The rank vector: ")
    print(r)
    
    diff=np.sum(abs(r-r_prev))
    if (diff<threshold):
        break
    
    r_prev=r

print("The final rank vector: ")
print(r[:, 0])

1 Comment

ACcretic

March 24, 2023

Great to learn . The case used to transfer knowledge is just helpful.